Типовые алгоритмы обработки массивов включают решения задач, связанных с заполнением, выводом элементов, сортировкой и поиском. Ниже приведены примеры таких алгоритмов для обработки одномерных массивов.
Заполнение
- Поочередный ввод элементов. Элементы массива вводятся поэлементно, обычно в порядке возрастания индексов. Для реализации алгоритма необходимо организовать цикл.
Инициализация массива — задание каждому элементу конкретного числового значения. Например, можно перечислить значения элементов в фигурных скобках через запятую: тип имя_переменной[размерность]={элемент_0, элемент_1, …}
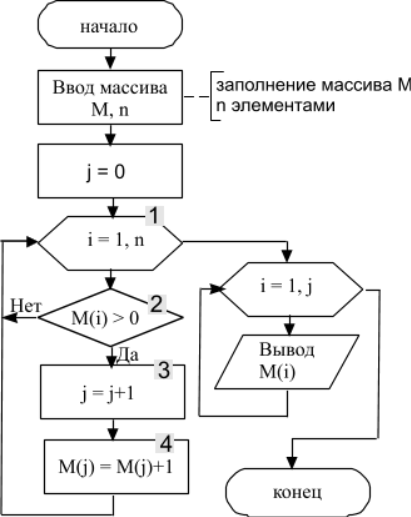
Вывод
- Поэлементный вывод. Элементы массива выводятся поэлементно, для чего также используется цикл. Элементы можно обрабатывать, двигаясь от начала массива к его концу или в обратном направлении.
- Вывод в строку. Например, в Бейсике алгоритм вывода элементов одномерного массива реализуется так:
for i=1 to n print a(i) ; » » ; next i. В Паскале — for i:=1 to n do write(a[i]).
Сортировка
- Пузырьковая сортировка. Простой алгоритм, сравнивающий соседние элементы и меняющий их местами. Подходит для небольших массивов.
- Быстрая сортировка. Разделяет массив на части, сортирует каждую часть и затем объединяет их. Эффективный алгоритм для больших массивов.
- Сортировка слиянием. Разделяет массив на части, сортирует каждую часть и затем объединяет их в отсортированный массив.
Поиск
- Линейный поиск. Проверяет каждый элемент массива по очереди. Подходит для небольших массивов.
- Бинарный поиск. Работает с отсортированным массивом, разделяя его пополам и проверяя средний элемент.
- Поиск с барьером. Предусматривает естественное ограничение просмотра элементов массива в виде барьера — элемента, обладающего заданными свойствами, который искусственно добавляется к массиву в начало или в конец. Если рассматривается алгоритм первого вхождения искомого элемента, то барьер устанавливается в конец массива, в случае поиска последнего вхождения (элементы проверяются, начиная с последнего) — в начало массива.
В общем случае алгоритм решения задачи с использованием массивов выглядит так, как показано на рис.2. Рассмотрим более подробно шаги этого алгоритма.
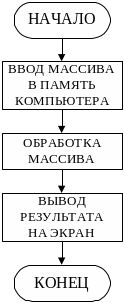
Рис.2
2.2.1. Ввод одномерного массива в память компьютера
При вводе массива предлагается, что память для его размещения уже зарезервирована. Количество элементов, под которые зарезервирована память, обозначим константой LEN. Тогда LEN — это максимально возможное для использования количество элементов массива (длина массива). В действительности, при решении большинства задач количество требуемых элементов может изменяться от одного запуска программы к другому. Поэтому следует предоставить пользователю возможность заказать требуемое ему в данном конкретном случае число элементов массива, которое обозначим N. Таким образом, первым шагом алгоритма ввода одномерного массива станет ввод переменной N — требуемой длины массива. Напомним, что N всегда меньше либо равна LEN.
В языке Паскаль нет средств ввода-вывода всего массива целиком, поэтому ввод и вывод массивов выполняется поэлементно. Словесно можно описать шаг ввода одномерного массива следующим образом:
ввести элемент А[1];
ввести элемент А[2];
….
ввести элемент А[N].
Т. о., индекс вводимого элемента изменяется от 1 до N с шагом 1. Очевидно, что для реализации ввода массива необходимо выбрать структуру цикла. Блок-схема ввода массива представлена на рис. 3.

Рис.3
На языке ТурбоПаскаль ввод одномерного массива реализуется следующим фрагментом программы:
Program ABC;
const
LEN = 100; {максимальная длина массива}
var
А : array [1. .LEN] of real; {объявление массива, состоящего из 100 вещественных чисел}
i,N : byte; {i — индекс, N — требуемая длина массива}
BEGIN
write (‘Введите длину массива N =’);
readln(N);
for i:=1 to N do
begin
write(‘A[‘ , i , ‘]=’ );
read (A [i])
end;
…
END.
В дальнейшем заголовок и раздел описания программы приводить не станем. Фрагменты программ, описанные в примерах, следует располагать в требуемом месте раздела исполняемых операторов приведённой здесь программы.
2.2.2. Вывод массива на экран
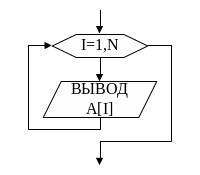
Блок-схема алгоритма вывода одномерного массива на экран представлена на рис.4. Она очень мало отличается от вышеприведённой блок-схемы алгоритма ввода и построена на основании таких же рассуждений. Единственным принципиальным отличием является то, что не требуется запрашивать у пользователя длину массива, которая к моменту вывода массива на экран уже известна.
Фрагмент программы для вывода одномерного массива на экран:
…
writeln(‘Массив А’);
for i:=1 to N do
write (A[ i ]:6:2);
writeln;
…
Рис.4
2.2.3. Подсчёт суммы, произведения, количества элементов одномерного массива, удовлетворяющих заданному условию
Для нахождения суммы элементов массива воспользуемся методом накопления. Для этого заведём дополнительную переменную S, к которой поочерёдно станем добавлять значения элементов массива. Т.к. при объявлении любой переменной на языке ТурбоПаскаль её значение не определено, необходимо занести в переменную S такое значение, которое не повлияет на конечный результат суммирования элементов массива. Этим значением является 0.
Далее необходимо к значению переменной S добавлять элементы массива с номерами 1, 2, …, N, т.е. выполнять следующие действия:
S = S +А[1]
S = S + A[2]
. . . . . . . . . . .
S = S + A[N]
Отсюда видно, что для вычисления суммы элементов массива необходимо использовать цикл, который будет повторять оператор S=S+A[i], где i поочерёдно принимает значения от 1 до N с шагом 1. После завершения N итераций цикла значение суммы будет вычислено окончательно и его можно обработать по условию задачи, например, вывести на экран.
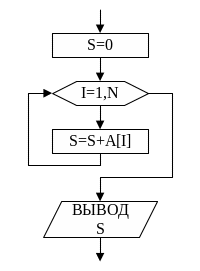
Блок-схема алгоритма нахождения суммы приведена на рис.5. Фрагмент программы записан ниже:
 • • •
• • •
S:=0;
for i:=1 to N do
S:=S+A[i];
writeln( Сумма S=’ , S);
• • •
Рис. 5
В случае, если необходимо найти сумму элементов, удовлетворяющих некоторым условиям (положительные, отрицательные, четные и т.п.), то в этом случае каждый элемент массива необходимо будет сравнивать с некоторым значением, заданным в условии задачи. На рис.6 представлена блок-схема алгоритма поиска суммы положительных значений элементов массива. В этом случае каждый элемент массива сравнивается с 0, и, если он больше 0, то он включается в сумму. Фрагмент программы приводится ниже.

…
S := 0;
for i :=1 to N do
if A[i] > 0 then
S := S + A[i];
writeln (‘S= ‘,S);
…
Рис. 6
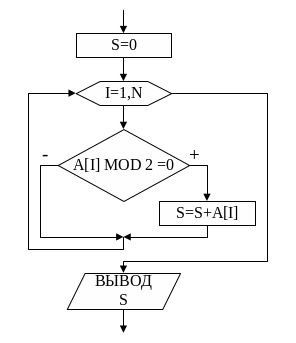
На рис.7 представлена блок-схема алгоритма поиска суммы четных элементов массива. Известно, что четные элементы делятся на 2 без остатка. В ТР существует математическая операция MOD, позволяющая определить остаток от деления числа а на некоторое число р: а MOD р. Следует заметить, что операнды а и р могут быть только целыми числами. Например,
4 MOD 2 = 0 ( т.к. 4 – четное число);
5 MOD 2 = 1 ( т.к. 5 – нечетное число);
7 MOD 3 = 1 ( т.к. 7 не кратно 3 ).
Фрагмент программы приводится ниже.
…
S := 0;
for i :=1 to N do
if A[i] MOD 2 = 0 then
S := S + A[i];
writeln (‘S= ‘,S);
…
Рис. 7
Аналогично следует вычислять произведение элементов массива, за исключением того, что в качестве начального значения произведения следует принять 1, т.к. именно умножение на 1 не повлияет на искомое произведение.
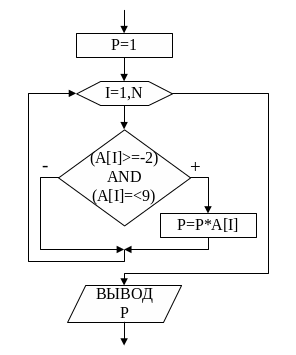
На рис.8 представлена блок-схема алгоритма поиска произведения Р элементов массива, попадающих в интервал от –2 до 9. Фрагмент программы приводится ниже.
…
P :=1;
for i:=1 to N do
if (A[i] >= -2) and (A[i] <= 9) then
P := P * A[i];
writeln(‘P= ‘, P);
…
Рис. 8
При нахождении количества элементов массива следует воспользоваться теми же рассуждениями, что и в ранее рассмотренных случаях. Обычно требуется подсчитать количество элементов, удовлетворяющих некоторым заданным условиям, например, количество положительных элементов. Для решения этой задачи поочерёдно сравним каждый элемент массива с 0, и при обнаружении отрицательного увеличим количество на 1. Когда все элементы массива закончатся, искомое количество будет окончательно подсчитано и его можно обработать по условию задачи.
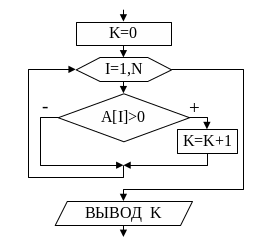
Блок-схема алгоритма нахождения количества отрицательных элементов представлена на рис.9. Фрагмент программы, соответствующий этой блок-схеме, приведён ниже.
К:=0;
for i:=1 to N do
if A[i]>0 then
K:=K+1;
writeln ( ‘Количество равно’, К);
Рис.9